نسبت های مثلثاتی به ارتباط بین زوایای یک مثلث قائم الزاویه با طول اضلاع آن می پردازد. مهم ترین علت اهمیت این بحث در فیزیک، پیدا کردن مولفه های کمیت های برداری در دستگاه مختصات متعامد است. ![]()
![]()
![]()
یک مثلث قائم الزاویه فرض کنید، برای سادگی اندازه ی وتر آن را برابر با 1 بگیرید:
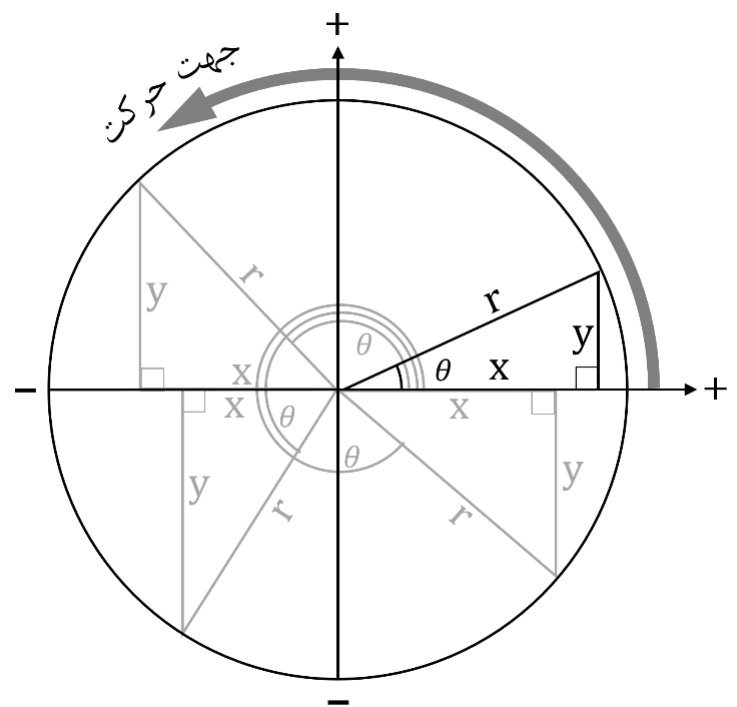
فرض کنید در شکل بالا، زاویه ی θ تغییر کند، به سادگی می توان متصور شد که نقطه A روی یک دایره حرکت می کند. این دایره را «دایره ی مثلثاتی» می نامیم. اندازه شعاع این دایره برابر با اندازه وتر یعنی 1 است:
اگر دایره مثلثاتی را تکمیل نماییم: ![]()
به دو ضلع دیگر مثلث توجه کنید. طبق قرارداد، با توجه به اندازه ی زاویه، برای مقادیر x و y طبق علامت های روی شکل، علامت مثبت یا منفی در نظر می گیریم.
مبنای اندازه گیری زاویه، سمت مثبت محور x ها است. همچنین اگر در خلاف جهت حرکت نشان داده شده در شکل حرکت کنیم، اندازه ی زاویه را منفی در نظر می گیریم.
تعریف جدیدی از اندازه زاویه
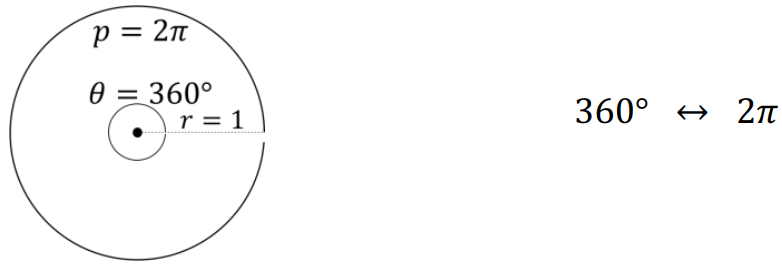
می دانیم محیط دایره از رابطه 2πr محاسبه می شود. برای دایره ی مثلثاتی، r=1 و در نتیجه محیط برابر با 2π خواهد بود. همچنین می دانیم اگر کل دایره را یک کمان در نظر بگیریم، این کمان زاویه 360 درجه خواهد داشت. اگر محیط دایره مثلثاتی را با اندازه ی زاویه کمان آن مقایسه کنیم، داریم:
در مورد یک نیم دایره، می دانیم محیط
نصف می شود و کمان آن 180 درجه است:
و در مورد ربع دایره، محیط، یک چهارم دایره ی کامل است و کمان آن 90 درجه است:
این عمل را می توان برای هر زاویه ی دیگری به همین ترتیب ادامه داد. مثلا:
این بیان جدید را رادیان می نامند. مثلا می گوییم 90 درجه برابر با π/2 رادیان است. این بیان، در محاسبات فیزیکی بسیار کارآمد است، چرا که زاویه را می توان در مقایسه با محیط دایره بیان کرد. دقت داشته باشید که رادیان بدون واحد است.
یک تمرین ساده: زوایای 30 درجه، 45 درجه و 60 درجه را بر حسب رادیان بیان کنید.
یک تمرین کمی پیچیده: وقتی می گوییم زاویه ای π/2 رادیان است، منظور این است که آن زاویه 90 درجه است. حال اگر بگوییم زاویه ای 1 رادیان است، منظور چیست؟ از شکل زیر کمک بگیرید:
یک تمرین بسیار کاربردی: تعریف جدید، یعنی رادیان، به ما کمک می کند که طول کمان طی شده را به راحتی به زاویه ی کمان نسبت دهیم. مثلا فرض کنید جسمی روی محیط دایره ای به شعاع r=10 m ، کمانی معادل زاویه ی θ=π/2 (بر حسب رادیان) را طی می کند. این جسم چه مسافتی را طی کرده است؟
تعاریف نسبت های مثلثاتی
نسبت اندازه ی ضلع روبه روی زاویه ی θ به وتر را سینوس می نامند:
نسبت اندازه ی ضلع مجاور زاویه ی θ به وتر را کُسینوس می نامند:
نسبت اندازه ی ضلع روبه روی زاویه ی θ به ضلع مجاور زاویه ی θ را تانژانت می نامند:
نسبت اندازه ی ضلع مجاور زاویه ی θ به ضلع روبه روی زاویه ی θ را کُتانژانت می نامند. کتانژانت عکس تانژانت است:
نکته کاربردی: به طور کلی لزومی ندارد اندازه وتر برابر با 1 باشد و برای هر مثلث قائم الزاویه ای، نسبت های مثلثاتی قابل محاسبه است. مقادیر نسبت های مثلثاتی برای یک زاویه ی مشخص، مستقل از اندازه ی وتر بوده و همیشه عددی ثابت است! مثلا به شکل زیر توجه کنید، مقدار سینوس را برای مثلث های مختلف که روی هم قرار گرفته اند محاسبه کنید. دقت کنید که در همه ی این مثلث ها، زاویه ی θ برابر است.
نکته جالب دوم: سینوس چو بر روی کسینوس نشیند، تانژانت به دست آید و بالعکس کتانژانت! (اثبات کنید!):
نکته حیاتی: برای محاسبه ی نسبت های مثلثاتی در مثلث هایی که چرخیده اند، به جای x و y، از مفاهیم «ضلع رو به رو» و «ضلع مجاور» استفاده کنید تا دچار سردرگمی نشوید!
تکلیف
مقادیر نسبت های مثلثاتی را می توان برای برخی از زاویه ها به سادگی محاسبه کرد، جدول زیر را پر کنید:
همچنین مقادیر نسبت های مثلثاتی برای زاوایای بزرگتر از 90 درجه یا زوایای منفی قابل محاسبه است، جدول زیر را پر کنید:
- طبقه بندی: صفحات راهنما








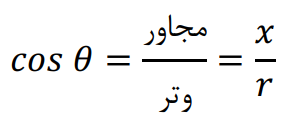
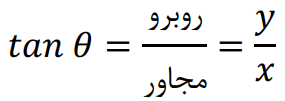





سلام و خداقوت خیلی عالی بود.